[프로그래머스] 자물쇠와 열쇠

 

https://programmers.co.kr/learn/courses/30/lessons/60059

코딩테스트 연습 - 자물쇠와 열쇠

---

-풀이-

먼저 key의 우측하단의 좌표를 (kx,ky) 라고 할것이다.

 

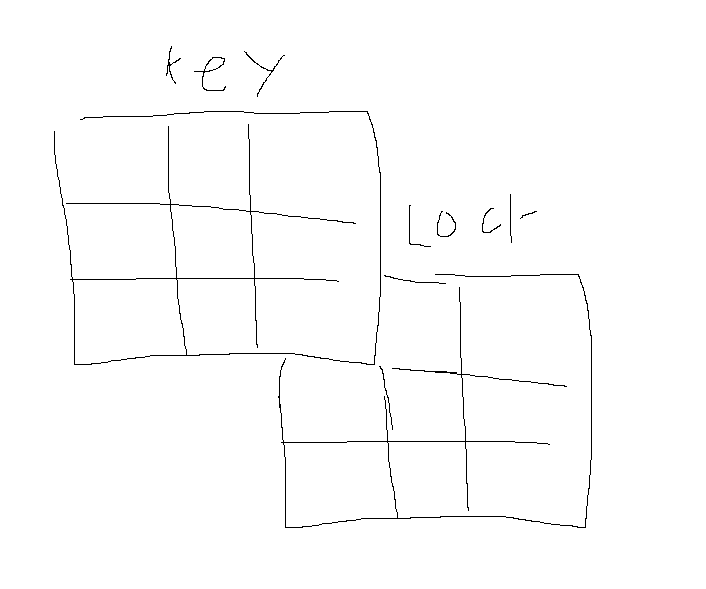
이런식으로 겹치기 시작하여,

이렇게 까지 겹쳐보며 열쇠가 맞는지 확인해볼것이다.

 

그럼 우측하단의 좌표가 kx,ky 라고하고, lock의 size를 n,key의 size를 m이라고 할때, kx와 ky의 범위는 각각 0~n+m-1까지 된다. 이러면 키를 꽃는 모든 경우의 수를 구할 수 있다.

 

그럼 키가 맞는지에 대해 어떻게 확인을 할까?

답은 간단하다. lock배열을 돌며, 만약 key와 겹쳐진 부분이라면 lock값에 key를 더해주고, 아니면 lock값만 보면된다.

이 값이 1이 아니라면, 해당칸은 돌기와 돌기가 만난 부분( 2가 된다.) 이거나, 키를 넣어도 홈인부분( 0이된다.)이 되기때문에, 현재 키의 배치는 열 수 없다는 결론이 나온다.

 

그럼 겹쳐진 부분인지 아닌지는 어떻게 판단할까?

현재 우측 하단의 좌표인 kx와 ky를 알고, 현재 탐색중인 lock의 좌표(x,y) 를 알고있다면 구할 수 있다.

key의 size를 k라고 한다면. 0 <= k-1-(kx-x) < k 이면서 , 0<= k-1-(ky-y) <k 를 만족했을때, 현재 탐색중인 lock위에 key가 겹쳐져있다는 뜻이된다. 따라서 저 범위안에 들어가면, key[ k-1-(kx-x) ] [ k-1-(ky-y) ] 값을 더해준뒤, 그 값이 1인지 아닌지 판별해주면된다.

 

이렇게 구했을때, 맞는 배치가 없다면, key를 시계방향으로 90도 회전시켜야한다.

90도 회전시키는 알고리즘은 아래와 같다.

int temp[21][21]={0};
for(int i=0;i<k+1;i++){
	for(int j=0;j<k+1;j++){
    	temp[j][k-i]=key[i][j];
    }
 }
 for(int i=0;i<k+1;i++){
 	for(int j=0;j<k+1;j++){
 		key[i][j]=temp[i][j];
 	}	
 }

이렇게 확인하고, 돌리고, 확인하고, 돌리고, 확인하고, 돌리고 를 반복하면서 모든경우를 탐색해본다.

 

-코드-

#include <string>
#include <vector>
#include<iostream>

using namespace std;


bool solution(vector<vector<int>> key, vector<vector<int>> lock) {
   int l=lock.size();
    int k=key.size()-1;
    for(int t=0;t<4;t++){
        for(int kx=0;kx<l+k;kx++){
            for(int ky=0;ky<l+k;ky++){
                bool flag=true;
                for(int x=0;x<l;x++){
                    if(!flag) break;
                    for(int y=0;y<l;y++){
                        int data=lock[x][y];
                        if(0<=k-(kx-x)&&k-(kx-x)<k+1 &&0<=k-(ky-y)&&k-(ky-y)<k+1){
                            data+=key[k-(kx-x)][k-(ky-y)];
                        }
                        if(data!=1){
                            flag=false;
                        }
                    }
                }
                if(flag){
                    return true;
                }
            }
        }

        int temp[21][21]={0};
        for(int i=0;i<k+1;i++){
            for(int j=0;j<k+1;j++){
                temp[j][k-i]=key[i][j];
            }
        }
        for(int i=0;i<k+1;i++){
            for(int j=0;j<k+1;j++){
                key[i][j]=temp[i][j];
            }
        }
    }
    return false;
}